


In the Alternative Investments industry, style analysis is commonly used to estimate the exposure of less transparent funds. Ordinary Least Square (OLS) is without doubt the most widely used and known regression technique used to explain the return streams of these funds.
In this article we will investigate heteroskedasticity, an issue that often arises in OLS regressions, and the measures that can be taken to account for it.
According to the Gauss-Markov theorem, for an OLS regression to produce BLUE (Best, Linear and Unbiased Estimators), 5 assumptions must be satisfied. One of them is homoskedasticity, which requires the variance of the error term to be constant.
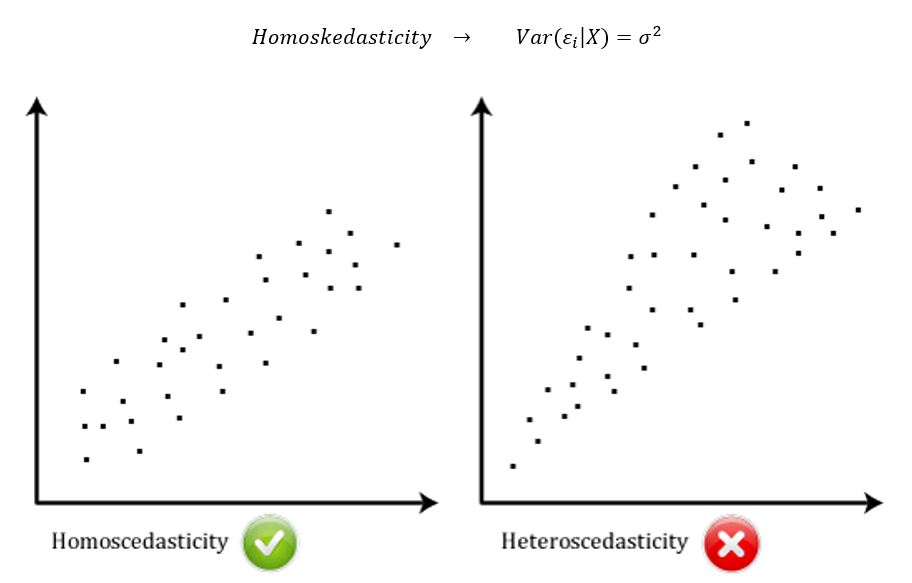
Figure 1 - Example of Homoscedastic and Heteroskedastic scatterplot
In practice, for most of the regressions this assumption does not hold, and the problem of heteroskedasticity needs to be addressed to preserve the validity of assertions made on the significance of our estimators.
The first step is to verify if this specific assumption of the Gauss-Markov theorem holds, by carrying out a Breusch-Pagan test or White test for heteroskedasticity. In a scenario where the regression does present heteroskedasticity two issues will need to be addressed.
The first is that the standard errors computed for the estimators will be biased and smaller than they should be. This means that the assertions made on whether the betas are significantly different than 0 may be biased. To solve this, it is suggested to compute robust White standard errors that will preserve the validity of t-statistics computed.
The second issue is that while the OLS estimators are still unbiased and consistent, they no longer are the best estimators of the population parameters. Using other methods such as Generalised Least Squares or Weighted Least Squares estimators will produce more efficient estimators than OLS and permanently solve the issue of heteroskedasticity.
To conclude, when using Ordinary Least Squares in style analysis, the issue of heteroskedasticity (i.e., variance of the error term being inconstant) is often overlooked. This is caused by inaccurate assertions about the significance of the beta estimators produced. A quick workaround this is to use robust standard errors for each of the betas. Alternatively, to eliminate the heteroskedasticity, one should opt for Generalised Least Squares or, more specifically Weighted Least Squares model.
Sources:
Wooldridge, Jeffrey M. Introductory Econometrics: A Modern Approach. Mason, OH: Thomson/South-Western, 2006.
N.B. This article does not constitute any professional investment advice or recommendations to buy, sell, or hold any investments or investment products of any kind, and should be treated as more of an illustrative piece for educational purposes.
To trial a truly powerful and comprehensive analytic software for investment decisions, fund allocation, and our new, innovative digital due diligence visit alternativesoft.com , call us on +44 20 7510 2003, or email us information@alternativesoft.com
71 Carter Lane, London
EC4V 5EQ
+44 20 7510 2003